Tirolian Skysled
(Version 1.02 - Last updated:
9/24/98)
- RPG Stats by Kenneth
Olson
- Background Information
derived from Robotech Technical
Files
-
BACKGROUND
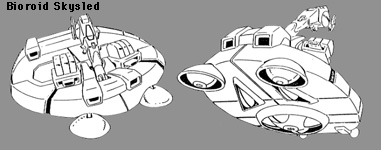
See Robotech Technical
Files. The
purpose of this entry is to create RPG stats for the skysled which are more in line with
the characteristics seen in Robotech.
RPG STATS
- Vehicle Type: One mecha transport sled
- Class: Skysled
Manufacturer: Robotech Masters
Crew: One bioroid. However, two may be carried under extreme conditions
 MDC BY LOCATION:
MDC BY LOCATION:
| Location |
MDC |
| (1) Main Body |
70 |
| Bioroid Controller |
25 |
| Anti-Gravity Units (3) |
25 |
| Ion-Guns (2) |
25 |
NOTES:
- Depleting the MDC of the main body will destroy the mecha
SPEEDS:
- FLYING:
- 415 kph in plantary atmospheres
-
STATISTICAL DATA:
- LENGHT:
- 9.4 m
- WIDTH:
- 4.1 m
- WEIGHT:
- 8.4 metric tons
- CARGO:
- One or Two bioroids
- POWER PLANT:
- 45 standard protoculture cells.
One anti-gravity system.
Two plasma turbines, max. output estimated at 0.9 MW.
- Propulsion in Spaceborne operations:
- One anti-gravity system.
- Delta V:
- Conditionally unlimited
- Generator Endurance:
- 500 hours of continual use

WEAPON SYSTEMS:
- Twin Ion pulse Cannons:
- PRIMARY PURPOSE: Assault/Defense
- SECONDARY PURPOSE: Anti-Aircraft
- RANGE: 6,000 ft (1800 m)
- DAMAGE: Single Bursts 1d4*10, or dual bursts 2d4*10
- RATE OF FIRE: Equal to the total number of H-to-H attacks
- PAYLOAD: Conditionally Unlimited. The ion cannons can shoot up to 25 short
burst in one minute before depleting its energy reserve. After which point the
weapons drum can only fire short bursts at a rate of 4 per melee until the energy reserve
is replenished
STANDARD EQUIPMENT FOR SKYSLED:
- RADAR : One spherical phased array radar with surveillance modes, effective range
over 245 km.
- OPTICS: NIGHTVISION: Range: 2000 feet (610 m). A passive light image intensifier
that emits no light of its own, but relies on ambient light which is electronically
amplified to produce a visible picture.
- OPTICS: THERMAL IMAGER: Range: 2000 feet (610 m). A passive optical heat sensor
that detects infrared radiation projected by warm objects and converts that data into a
false-color visible image. The system enables the pilot to see in the dark, in shadows,
and through smoke, and also adds a +10% bonus to pilots using a tracking skill.
- ACTIVE PASSIVE JAMMING SYSTEMS: These systems can be used to jam both
sensors and missiles.
COMBAT BONUSES FOR Bioroid Training:
To all Bioroids
- +2 to strike with ion guns, no other bonuses apply
- +5 to Dodge
SOURCES USED IN CREATION OF DOCUMENT
- Palladium's Robotech RPG Book IV: Southern Cross
- The Robotech Technical Files: Skysled
Back to Mecha Home


 MDC BY LOCATION:
MDC BY LOCATION: 